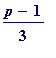 ) such that
) such that
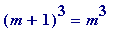 (mod
p
), and in connection with that I was hoping to get an insight by examining some actual cases...
(mod
p
), and in connection with that I was hoping to get an insight by examining some actual cases...
The (beautiful) cube-square relationship
Here would not be the place to detail all the ideas that occurred to me as possible proofs, though I can say that none of them worked... The good news for me, though, was that one of my failed attempts led me quite by chance to a lovely discovery (to me at any rate: I considered it then the most beautiful mathematiocal experience I had ever had by myself ), with an obviously powerful theoretical and computational consequence , as I'll explain shortly. (For Dublin-based readers: the germ of the idea occurred to me while having coffee in Panem , on the north quays, beside the millennium bridge)
At one point I became fixated with the belief that I would somehow get a proof through considering consecutive modular cubes (and their multiples...), meaning values of
m
(in the range 1 to
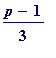 ) such that
) such that
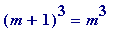 (mod
p
), and in connection with that I was hoping to get an insight by examining some actual cases...
(mod
p
), and in connection with that I was hoping to get an insight by examining some actual cases...
Quite suddenly something jumped out at me in connection with the cubic residues for the prime
p
= 331 (here
![]() = (2) (3) (5) (11) ):
= (2) (3) (5) (11) ):
> p := 331: seq(k^3 mod p, k = 1..(p-1)/3);
![]()
![]()
![]()
![]()
>
Those consecutive 7's are
![]() (mod 331) and
(mod 331) and
![]() (mod 331) (by the way it then follows that the modular ratio of one of them - either
(mod 331) (by the way it then follows that the modular ratio of one of them - either
![]() mod 331 or
mod 331 or
![]() mod 331 - must be the value of P[1, 3](331), if
it
isn't 1), and what
struck me
was
their connection
to the
final cubic residue
:
mod 331 - must be the value of P[1, 3](331), if
it
isn't 1), and what
struck me
was
their connection
to the
final cubic residue
:
that '49'
-
a square
- (which is of course
![]() mod 331) is
their product
mod 331) is
their product
Of course I started checking all the Jacobi primes that I already had, and in every single case it happened that the above phenomenon held... (rush of blood to the head...)
__________________
Aside
. I should relate that the occurrence of that
actual square
as the residue of
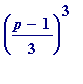 mod
p
struck me as being
highly significant
, as I'll try to explain: it happens to be immediate that for
all
primes p = 1 (mod 3) - and
not simply
the ones that are here of interest to us, the Jacobi ones - one
automatically
has
mod
p
struck me as being
highly significant
, as I'll try to explain: it happens to be immediate that for
all
primes p = 1 (mod 3) - and
not simply
the ones that are here of interest to us, the Jacobi ones - one
automatically
has
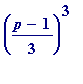 =
some square
(mod
p
)
=
some square
(mod
p
)
Incidentally that's because (you'll have to ignore this if you don't know about quadratic residues , and the circumstances in which -1 is/isn't a quadratic residue a prime p ) of a banality:
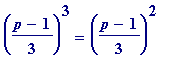 * (
* (
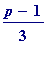 )
)
from which it follows that (ignore this if you don't know about quadratic residues)
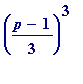 is automatically a quadratic residue for prime
p
= 1 (mod 3), since it's precisely for such primes that
is automatically a quadratic residue for prime
p
= 1 (mod 3), since it's precisely for such primes that
![]() is a quadratic residue... [end of Aside.]
is a quadratic residue... [end of Aside.]
____________________
But my gut feeling would have been that the ' some square ' would have a numerical value greater than the dividing modulus p , and be most unusual that it have an actual value less than p .
The immediate (highly significant) question then was : does this phenomenon characterise Jacobi primes (at that stage, only those of order 1 or 3; those of order 9 hadn't yet made their appearance...). Meaning? Can it be decided that a prime p = 1 (mod 3) is a Jacobi prime of order 1 or 3 merely by checking if
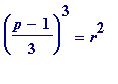 (mod
p
)
(mod
p
)
for some integer
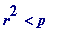 .
.
I thought that would be 'too good to be true', but nevertheless it needed investigating. In the following, then, this is what's going on:
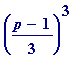 mod
p
is an
actual
square (that's the
and issqr(((ithprime(k)-1)/3)^3 mod ithprime(k))
)
mod
p
is an
actual
square (that's the
and issqr(((ithprime(k)-1)/3)^3 mod ithprime(k))
)
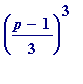 mod
p
is automatically less than
p
because of Maple's own choice of remainder.
mod
p
is automatically less than
p
because of Maple's own choice of remainder.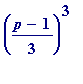 mod
p
(
will it/won't it be 1
?...)
mod
p
(
will it/won't it be 1
?...)> restart;
>
P[1,3] := proc(p) local r, k; r := 1;
for k from 2 to (p-1)/3 do
r := mods(r*k, p) od; r; end:
>
count:= 0:
for k from 2 to 1001 do
if ithprime(k) mod 3 = 1
and issqr(((ithprime(k)-1)/3)^3 mod ithprime(k))
then count := count+1:
p[count] := ithprime(k):
N[count] := ((ithprime(k)-1)/3)^3:
fi; od;
array([[p, `((p-1)/3)^3 mod p`, `P[1,3](p)^3 mod p`],
seq([p[k], N[k] mod p[k], P[1,3](p[k])^3 mod p[k]], k=1..count)]);
^3 mod p...](images/reduced TCD talk 9th Feb 2005177.gif)
>
Ah, those non 1's in the third column... Heartbreak or not? Well, yes, but just for a fleeting moment... for it jumped out at me (what a happy moment that was!) that the 1's and non 1's corresponded to the actual squares being odd and even !! It was such a perfect fit it simply had to be true ...
I thus had a new (to me) conjecture
: A prime
p
= 1 (mod 3) is a Jacobi prime of order 1 or 3 if and only if
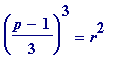 (mod
p
) for some
odd
square
(mod
p
) for some
odd
square
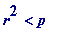
At the time, not having the remotest idea how to prove this, I nevertheless set about testing it beyond the range that I had already systematically tested, which at that time (Sat 11th Dec 2004) had taken several days to get up as far at 3.5 million . Then, in one 24 hour period, I was able to use the above conjecture to test ab initio up to 33.675 million, and every single one of the 246 produced primes were Jacobi of order 1 or 3 [that's saved in #1 cube-sq.mws].
While this was certainly exciting to me, it didn't satisfy me with respect to the privately-named inexplicable primes, although such primes somehow came in under the cube-odd square umbrella... Only later - on the evening of Wed 15th Dec - did the fog finally lift on those primes.
_____________________
Here's a modification to select only those corresponding to an odd square (that's achieved with the use of and... mod 2 = 1 ). Notice how I've been able to allow the live testing - during my talk - of the first ten thousand primes without getting into time difficulties). Notice that the odd squares increase monotonically...:
>
count:= 0:
for k from 2 to 10001 do
if ithprime(k) mod 3 = 1
and issqr(((ithprime(k)-1)/3)^3 mod ithprime(k))
and (((ithprime(k)-1)/3)^3 mod ithprime(k)) mod 2 = 1
then count := count+1:
p[count] := ithprime(k):
N[count] := ((ithprime(k)-1)/3)^3:
fi; od;
array([[p, `((p-1)/3)^3 mod p`, `P[1,3](p)^3 mod p`],
seq([p[k], N[k] mod p[k], P[1,3](p[k])^3 mod p[k]], k=1..count)]);
^3 mod p...](images/reduced TCD talk 9th Feb 2005180.gif)
>
Here's a modification to select only those primes corresponding to an
even square
(which it seemed to me must have some independent interest... they did...), achieved with the use of
and ... mod 2 = 0
). Notice that the even squares appear to fluctuate up and down, and indeed so too do the third column values of
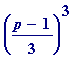 mod
p
(only later did I come to understand why that was happening:
seven quadratics
come into play...):
mod
p
(only later did I come to understand why that was happening:
seven quadratics
come into play...):
>
count:= 0:
for k from 2 to 10001 do
if ithprime(k) mod 3 = 1
and issqr(((ithprime(k)-1)/3)^3 mod ithprime(k))
and (((ithprime(k)-1)/3)^3 mod ithprime(k)) mod 2 = 0
then count := count+1:
p[count] := ithprime(k):
N[count] := ((ithprime(k)-1)/3)^3:
fi; od;
array([[p, `((p-1)/3)^3 mod p`, `P[1,3](p)^3 mod p`],
seq([p[k], N[k] mod p[k], P[1,3](p[k])^3 mod p[k]], k=1..count)]);
^3 mod p...](images/reduced TCD talk 9th Feb 2005182.gif)
>
Proposition 1
. A prime
p
= 1 (mod 3) satisfies
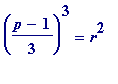 (mod
p
) for some
odd
square
(mod
p
) for some
odd
square
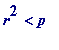 if, and only if,
if, and only if,
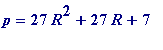 for some integer
for some integer
![]() .
.
Proof
. Suppose prime
p
= 1 (mod 3) satisfies
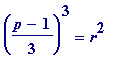 (mod
p
) for some odd square
(mod
p
) for some odd square
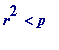 .
.
Then
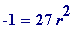 (mod
p
), giving
(mod
p
), giving
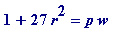 , some integer
w
with
, some integer
w
with
![]() . Now, since
r
is odd,
. Now, since
r
is odd,
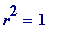 (mod 8) and
(mod 8) and
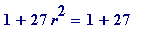 = 4 (mod 8), giving 4 divides
pw
, but 8 not dividing
pw
.
= 4 (mod 8), giving 4 divides
pw
, but 8 not dividing
pw
.
Hence
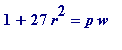 =
p
(4
W
),
W
odd and
=
p
(4
W
),
W
odd and
![]() . In fact
W
= 1, since any odd prime
q
dividin
g W
would divide
. In fact
W
= 1, since any odd prime
q
dividin
g W
would divide
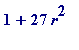 , and so would satisfy
q
= 1 (mod 6). Thus
, and so would satisfy
q
= 1 (mod 6). Thus
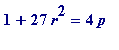 (instantly recognisable to anyone who knows the Gauss representation theorem, for primes
p
= 1 (mod 3)) and setting
r
= 2
R
+1 gives
(instantly recognisable to anyone who knows the Gauss representation theorem, for primes
p
= 1 (mod 3)) and setting
r
= 2
R
+1 gives
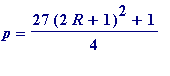 =
=
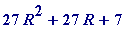
Conversely
, suppose
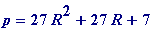 for some integer
for some integer
![]() . Then one has the following (beautiful)
identity
:
. Then one has the following (beautiful)
identity
:
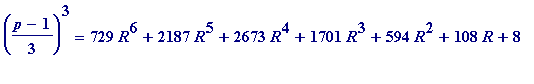
=
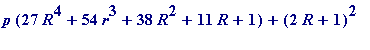
Proposition 2
. A prime
p
= 1 (mod 3) satisfies
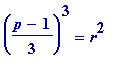 (mod
p
) for some
even
square
(mod
p
) for some
even
square
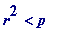 if, and only if,
if, and only if,
![]() (where the {
(where the {
![]() } are
seven
quadratics (which I've placed in a special section at the end), all of which, incidentally, have discriminant
} are
seven
quadratics (which I've placed in a special section at the end), all of which, incidentally, have discriminant
![]() ) for some integer
) for some integer
![]() .
.
Remark
. The first (in a sense) of those seven quadratics is
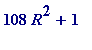 , and its prime values {
p
} have a very special property: they are
precisely
the primes for which
, and its prime values {
p
} have a very special property: they are
precisely
the primes for which
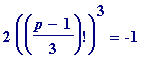 (mod
p
)
(mod
p
)
Alternatively (and better expressed), they are precisely the primes for which
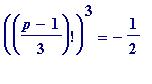 (mod
p
)
(mod
p
)
where the '
![]() ' is interpreted in the normal modular way (the
multiplicative inverse
of 2, modulo
p
)
' is interpreted in the normal modular way (the
multiplicative inverse
of 2, modulo
p
)
I have an entire infinite chain of such results (with their corresponding quadratics, one for each n in the following), dealing with
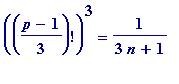 (mod
p
)
(mod
p
)
n
chosen from:
![]() , so that the original question corresponds to n = 0, and '
, so that the original question corresponds to n = 0, and '
![]() ' corresponds to
n
= -1.
' corresponds to
n
= -1.